By Richard R. Joss
This 2011 Annual Meeting panel discussion featured Dr. Alex Kane, Professor of Finance at UCSD and one of the coauthors of the widely used finance textbook, Essentials of Investments; and Richard Joss, the former Resource Actuary for Watson Wyatt Worldwide (now Towers Watson) and the author of three published technical papers on the above topic. The answer to the question posed is an important one because the Actuarial Standards Board is considering an amendment to Actuarial Standard of Practice No. 27, Selection of Economic Assumptions for Measuring Pension Obligations, which would specifically recognize the arithmetic mean of historical investment returns as an element for consideration by a pension actuary when selecting an investment return assumption for pension plan valuation purposes. While the two panelists disagreed with each other in many respects, they did agree that the proposed change to the Actuarial Standard of Practice No. 27 should not be adopted. A brief summary of each presentation is as follows.
Alex Kane
Dr. Kane pointed out that the arithmetic average is always larger than the geometric average, and that the difference is not trivial. He emphasized that if the true mean of an investment distribution were known, then this known mean could be used for forecasting, but then went on to note that the true mean is never known and must be estimated from historical data. He proposed that for forecasting purposes a smaller number than the arithmetic mean should be used.
He offered that the reason for selecting a smaller number is that any sample contains an estimation error, and that in this case estimation errors are asymmetric. The estimation error tends to compound upward as the investment horizon increases. Dr. Kane stated that because of this problem, the arithmetic average over-estimates the true mean, and that the size of the over-estimation increases with the investment horizon (H), but is improved when a longer history (T) is used. With this as background, he proposed the following formula for use in estimating the geometric mean for an investment horizon of H periods when one is using an investment history of T periods.
E(GH) = (GT)x(H/T) + (AT) x[(T-H)/T]
In this formula, GT is the geometric average for the T-period history, and AT is the arithmetic average for the T-period history. He then presented a graphical illustration to demonstrate how the proposed formula compared with a simulated investment history.
He went on to observe that log normal forecasting models are still not in synch with actual practice, and that actuaries need to be aware of three key consequential issues: jumps, changing risk (standard deviation), and changing mean. He closed by emphasizing that with lognormal distributions there is no question that risk in terminal wealth values is proportional to the time horizon. He noted that the widely held belief that stocks are less risky in the long run is wrong. He encouraged actuaries to base contribution requirements on the real risk-free rate of return.
Richard Joss
I took a different approach than Dr. Kane by first emphasizing that any given investment history actually has lots of different possible arithmetic means, and that as noted above, all of these various arithmetic means are larger than the actual rate of wealth growth achieved by the investment, which is the geometric mean. An example was provided by using data from the 2008 SBBI Yearbook. The example showed an investment that grew from $1 on January 1, 1926, to $15,091 on December 31, 2007. The actual rate of wealth growth (geometric mean) over the entire 82-year period was 12.45 percent. If this history is divided into 82 calendar years, the arithmetic average of these 82 individual returns becomes a much larger 17.08 percent. But the same history can be divided into fiscal years ending in March (with proper adjustment for the short periods at the beginning and end of the 82-year period) to yield an arithmetic average of 19.35 percent. When the same history is divided using fiscal years ending in October, the arithmetic average is 15.84 percent. I then asked the question: Which of these three numbers would an actuary use as the "best estimate?"
As any investment grows, it must leave behind a "tail" of returns, and the arithmetic mean of such a "tail" must always be larger than the actual rate of wealth growth. If an investment loses 50 percent one year, it will need to grow at a 100 percent rate for the next year just to get the investor back to where he or she started. This two-year investment will leave behind an arithmetic mean "tail" of 25 percent, but will provide a return of 0 percent to the actual investor over the two-year period.
The theory behind using the arithmetic mean is that historical returns may be treated as independent or uncorrelated events. Although there are statistical studies to support this assumption, I offered two challenges. The first challenge was to ask the question: What is the likelihood that the Dow Jones Industrial Average (DJIA) will not have losses for nine consecutive days? When treated as independent/uncorrelated events, the answer is the same as if the DJIA daily returns were treated as coin flips–heads the average goes up, tails the average goes down. For the next nine days the probability of not having nine loss days becomes 511/512 or 99.8 percent.
I then considered the possibility of not having nine days of consecutive losses for longer periods, ending with a stated probability of .00001 percent (1 in 10,000,000) for this event over a 33-year time horizon. After the session, it was pointed out to me that I made an error in the calculation. I compounded the result for each new investment day, when I should have only compounded the result for each new investment day that follows a day when the DJIA had a positive return. This changes the probability of not having a period of 9 negative days in a row over a 33-year period to .03 percent (1 in 3,000). The event is still rare, and the importance of the 33-year period is that the DJIA last experienced a nine-day losing streak in February, 1978. The point of the illustration was to consider the possibility that the daily DJIA returns might not be as uncorrelated as previously thought. I want to apologize for the error, and thank Jim Gannon and Robert Collie of Russell Investments for pointing out the problem.
The other illustration to cast doubt on the assumed independence/non-correlation of returns was to compare the commonly used lognormal distribution with an actual history of monthly results from the 2008 SBBI Yearbook. The commonly used lognormal assumption would call for 14 percent of large company stock returns to be between -0.2 percent and 1.8 percent for the month, when the actual history has 19 percent of monthly returns in this range. As a second example, the actual history only had 12 percent of the months with returns in excess of 5.8 percent, whereas the commonly used lognormal assumption anticipates 19 percent of monthly returns will be this large. When the commonly used lognormal density function is replaced with a density function designed to recognize the possible conditional nature of historical investment return data, the "match" improves considerably.
Finally, a specific formula was provided to estimate how much larger the arithmetic average would be when compared with the geometric average, when both averages are taken from an actual history. This formula, where n is the length of the history, k is the sample size, and the sigma is the standard deviation parameter from the lognormal distribution, is as follows:
Formula for Excess Arithmetic Mean
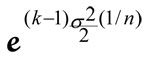
As an example of how the formula is used, for the period 1926-1945, average large stock returns were 7.13 percent. For the next 20 years (1946-1965) the average returns were 13.84 percent. For the period 1966-1986 returns averaged 8.66 percent, and for the period 1986-2005, returns averaged 11.93 percent. The arithmetic mean of these four numbers is 10.39 percent, and the geometric mean is 10.36 percent. The difference between these numbers is .03 percent. The formula value for a sample of size k = 4 is .05 percent. Additional illustrations were included in the session, and attendees were reminded one last time that the higher arithmetic means added nothing to the overall wealth. These higher arithmetic averages were just a byproduct of the actual process of wealth growth.
Summary
The arithmetic mean/geometric mean debate is sure to continue. The relatively large audience who attended this session seemed to pay close attention to both speakers–a sign of the importance of the answer to the question: Is the Arithmetic Mean of Past Returns the Best Estimate for the Future? And keep in mind, that while the speakers differed on several points, they both concurred that the answer to the question is probably no.
Richard Joss, FSA, PhD, is the former Resource Actuary for Watson Wyatt Worldwide (now Towers Watson). He can be reached at rrjoss@comcast.net.