 I am excited to introduce a new feature to CompAct. Beginning with this issue, we will be including excerpts from Secrets of Mental Math: The Mathemagician's Guide to Lightning Calculation and Amazing Math Tricks by Arthur Benjamin and Michael Shermer. Random House, Inc., was kind enough to give us permission to reproduce a selection from this book each quarter in CompAct. Much of the knowledge to be gained from this book depends on accumulating some skills in the earlier chapters; however, I will try to include sections that stand on their own. The selection below includes a simplified method to calculate the square of a two-digit number, based on some basic algebra.
I am excited to introduce a new feature to CompAct. Beginning with this issue, we will be including excerpts from Secrets of Mental Math: The Mathemagician's Guide to Lightning Calculation and Amazing Math Tricks by Arthur Benjamin and Michael Shermer. Random House, Inc., was kind enough to give us permission to reproduce a selection from this book each quarter in CompAct. Much of the knowledge to be gained from this book depends on accumulating some skills in the earlier chapters; however, I will try to include sections that stand on their own. The selection below includes a simplified method to calculate the square of a two-digit number, based on some basic algebra.
—Paul Ramirez, co-editor
Squaring numbers in your head (multiplying a number by itself) is one of the easiest yet most impressive feats of mental calculation you can do. I can still recall where I was when I discovered how to do it. I was 13, sitting on a bus on the way to visit my father at work in downtown Cleveland. It was a trip I made often, so my mind began to wander. I’m not sure why, but I began thinking about the numbers that add up to 20, and I wondered, how large could the product of two such numbers get?
I started in the middle with 10 × 10 (or 102), the product of which is 100. Next, I multiplied 9 × 11 = 99, 8 × 12 = 96, 7 × 13 = 91, 6 × 14 = 84, 5 × 15 = 75, 4 × 16 = 64, and so on. I noticed that the products were getting smaller, and their difference from 100 was 1, 4, 9, 16, 25, 36, … —or 12, 22, 32, 42, 52, 62, … ( see table below).
| Numbers that add to 20 | Distance from 10 | Their product | Product’s difference from 100 | |
|---|---|---|---|---|
| 10 | 10 | 0 | 100 | 0 |
| 9 | 11 | 1 | 99 | 1 |
| 8 | 12 | 2 | 96 | 4 |
| 7 | 13 | 3 | 91 | 9 |
| 6 | 14 | 4 | 84 | 16 |
| 5 | 15 | 5 | 75 | 25 |
| 4 | 16 | 6 | 64 | 36 |
| 3 | 17 | 7 | 51 | 49 |
| 2 | 18 | 8 | 36 | 64 |
| 1 | 19 | 9 | 19 | 81 |
I found this pattern astonishing. Next I tried numbers that add to 26 and got similar results. First I worked out 132 = 169, then computed 12 × 14 = 168, 11 × 15 = 165, 10 × 16 = 160, 9 × 17 = 153, and so on. Just as before, the distances these products were from 169 were 12, 22, 32, 42, and so on (see table below).
There is actually a simple algebraic explanation for this phenomenon (see Why These Tricks Work). At the time, I didn’t know my algebra well enough to prove that this pattern would always occur, but I experimented with enough examples to become convinced of it.
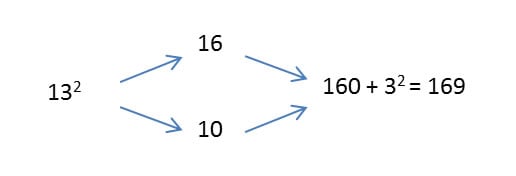
Then I realized that this pattern could help me square numbers more easily. Suppose I wanted to square the number 13. Instead of multiplying 13 × 13,
| Numbers that add to 26 | Distance from 13 | Their product | Product’s difference from 169 | |
|---|---|---|---|---|
| 13 | 13 | 0 | 169 | 0 |
| 12 | 14 | 1 | 168 | 1 |
| 11 | 15 | 2 | 165 | 4 |
| 10 | 16 | 3 | 160 | 9 |
| 9 | 17 | 4 | 153 | 16 |
| 8 | 18 | 5 | 144 | 25 |
Why not get an approximate answer by using two numbers that are easier to multiply but also add to 26? I chose 10 × 16 = 160. To get the final answer, I just added 32 = 9 (since 10 and 16 are each 3 away from 13). Thus, 132 = 160 + 9 = 169. Neat!
This method is diagrammed as follows:
Now let’s see how this works for another square:
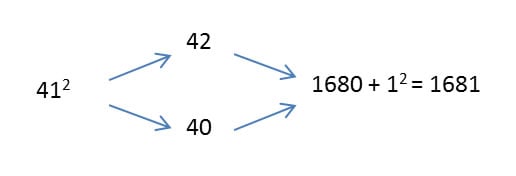
To square 41, subtract 1 to obtain 40 and add 1 to obtain 42. Next multiply 40 × 42. Don’t panic! This is simply a 2-by-1 multiplication problem (specifically, 4 × 42) in disguise. Since 4 × 42 = 168, 40 × 42 = 1680. Almost done! All you have to add is the square of 1 (the number by which you went up and down from 41), giving you 1680 + 1 = 1681.
Can squaring a two-digit number be this easy? Yes, with this method and a little practice, it can. And it works whether you initially round down or round up. For example, let’s examine 772, working it out both by rounding up and by rounding down:
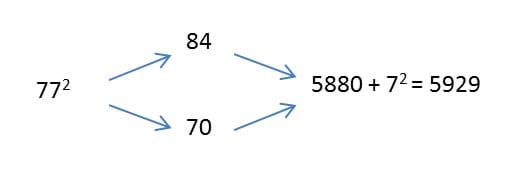
Or
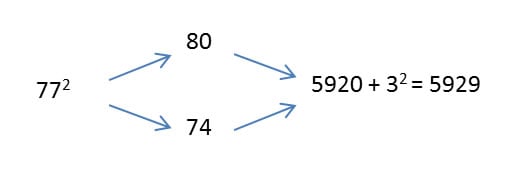
In this instance the advantage of rounding up is that you are virtually done as soon as you have completed the multiplication problem because it is simple to add 9 to a number ending in 0!
In fact, for all two-digit squares, I always round up or down to the nearest multiple of 10. So if the number to be squared ends in 6, 7, 8 or 9, round up, and if the number to be squared ends in 1, 2, 3 or 4, round down. (If the number ends in 5, you do both!) With this strategy you will add only the numbers 1, 4, 9, 16 or 25 to your first calculation.
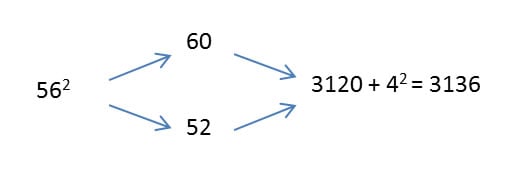
Let’s try another problem. Calculate 562 in your head before looking at how we did it, below:
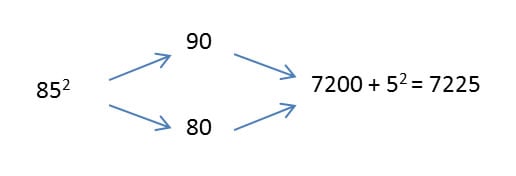
Squaring numbers that end in 5 is even easier. Since you will always round up and down by 5, the numbers to be multiplied will both be multiples of 10. Hence, the multiplication and the addition are especially simple. We have worked out 852 and 352, below:

As you saw in Chapter 0, when you are squaring a number that ends in 5, rounding up and down allows you to blurt out the first part of the answer immediately and then finish it with 25. For example, if you want to compute 752, rounding up to 80 and down to 70 will give you “Fifty-six hundred and … twenty-five!”
For numbers ending in 5, you should have no trouble beating someone with a calculator, and with a little practice with the other squares, it won’t be long before you can beat the calculator with any two-digit square number. Even large numbers are not to be feared. You can ask someone to give you a really big two-digit number, something in the high 90s, and it will sound as though you’ve chosen an impossible problem to compute. But, in fact, these are even easier because they allow you to round up to 100.
Let’s say your audience gives you 962. Try it yourself, and then check how we did it.
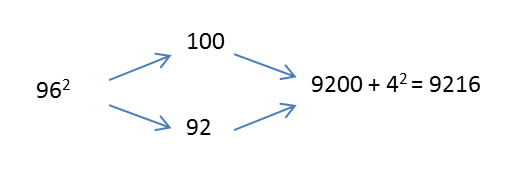
Wasn’t that easy? You should have rounded up by 4 to 100 and down by 4 to 92, and then multiplied 100 × 92 to get 9200. At this point you can say out loud, “Ninety-two hundred,” and then finish up with “sixteen” and enjoy the applause!
Why These Tricks Work
This section is presented for teachers, students, math buffs and anyone curious as to why our methods work. Some people may find the theory as interesting as the application. Fortunately, you need not understand why our methods work in order to understand how to apply them. All magic tricks have a rational explanation behind them, and mathemagical tricks are no different. It is here that the mathemagician reveals his deepest secrets!
In this chapter on multiplication problems, the distributive law is what allows us to break down problems into their component parts. The distributive law states that for any numbers a, b and c:
(b + c) × a = (b × a) + (c × a)
That is, the outside term, a, is distributed, or separately applied, to each of the inside terms, b and c. For example, in our first mental multiplication problem of 42 × 7, we arrived at the answer by treating 42 as 40 + 2, then distributing the 7 as follows:
42 × 7 = (40 + 2) × 7 = (40 × 7) + (2 × 7) = 280 + 14 = 294
You may wonder why the distributive law works in the first place. To understand it intuitively, imagine having 7 bags, each containing 42 coins, 40 of which are gold and 2 of which are silver. How many coins do you have altogether? There are two ways to arrive at the answer. In the first place, by the very definition of multiplication, there are 42 × 7 coins. On the other hand, there are 40 × 7 gold coins and 2 × 7 silver coins. Hence, we have (40 × 7) + (2 × 7) coins altogether. By answering our question two ways, we have 42 × 7 = (40 × 7) + (2 × 7). Notice that the numbers 7, 40 and 2 could be replaced by any numbers (a, b or c) and the same logic would apply. That’s why the distributive law works!
Using similar reasoning with gold, silver and copper coins we can derive:
(b + c + d) × a = (b × a) + (c × a) + (d × a)
Hence, to do the problem 326 × 7, we break up 326 as 300 + 20 + 6, then distribute the 7, as follows: 326 × 7 = (300 + 20 + 6) × 7 = (300 × 7) + (20 × 7) + (6 × 7), which we then add up to get our answer. As for squaring, the following algebra justifies my method. For any numbers A and d
A2 = (A + d) × (A – d) + d2
Here, A is the number being squared; d can be any number, but I choose it to be the distance from A to the nearest multiple of 10. Hence, for 772, I set d = 3 and our formula tells us that 772 = (77 + 3) × (77 − 3) + 32 = (80 × 74) + 9 = 5929. The following algebraic relationship also works to explain my squaring method:
(z + d)2 = z2 + 2zd + d2 = z( z + 2d) + d2
Hence, to square 41, we set z = 40 and d = 1 to get:
41² = (40 + 1) 2 = 40 × (40 + 2) + 12 = 1681
Similarly, (z − d)2 = z( z − 2d) + d2
To find 772 when z = 80 and d = 3,
77² = (80 − 3)2 = 80 × (80 − 6) + 32 = 80 × 74 + 9 = 5929