By Dave Snell
Any General Insurance (GI) actuary who has not been living under a rock for the past several years has heard of predictive modeling, data analytics, Big Data, and several related terms. In fact, GI actuaries have quickly embraced these concepts and techniques in practice. You can be proud to have been the leading edge of the newer actuarial analytics. Most of you may feel that an awareness of classification and regression techniques is a necessary skill for today’s GI actuary.
I submit that it is necessary, but not sufficient.
The world today is a lot more complex than it used to be; and the need to employ complexity sciences may become as necessary next week as classification and regression are today.
But what are complexity sciences? In the spring of 2010, I attended a week-long conference held by world leaders in complexity sciences, and they could not even agree upon the definition of complexity. In fact, they did not even agree whether the associated study of it was a singular (complexity science) or plural (complexity sciences) term! Complexity, somewhat like pornography, is often easier to recognize than to define.1
Why should you care about this? Some of you are already an FSA or FCAS. So clearly the need for any more knowledge is over, right? You should care because according to Stephen Hawking, “Complexity is the new science for this century”; and because by studying the broad topics of complexity, we can better understand the narrower topics of actuarial pricing and modeling. I believe that those who master this new area will have advantages over those who just can’t figure out where we are going with all of this.
| “The people who master the new sciences of complexity will become the economic, cultural, and political superpowers of the next century.”— Heinz Pagels, president of the International League for Human Rights. |
Back when the world was bit simpler, before computers became ubiquitous parts of our lives (PCs, smart phones, intelligent appliances, etc.), actuaries used commutation functions for “advanced” risk calculations. Years before commutation functions, slide rules facilitated state-of-the art modeling capabilities. The first space rocket launches used slide rules and tables of logarithms to go where man had never gone before.
Now, we look back upon these somewhat primitive tools and wonder how they could have been considered sufficient at the time; but in doing so, we overlook just how much less complicated our lives were prior to the internet, television, computers, and much of what we take for granted today. I watched one of my grandchildren recently become frustrated by a hardbound book because he was unable to pinch and zoom the pictures on the printed page.
In this article, I can only touch upon a tiny subset of the many topics I consider part of complexity sciences. If you want more information, please let me know; and please consider some of the references I suggest later.
Evolutionary Computation: learning from nature
If you place an ant, or a termite, on a tabletop and watch it move around aimlessly, it is clear that they are not the brainiacs of the animal kingdom. An ant seems to lack free will and a sense of self. In fact, a single ant or termite cannot survive outside of its colony.
Some scientists argue that we should think of the ant colony as an animal rather than the individual ants. The ants are like cells making up the body of the animal. In an ant colony, even the queen is not a ruler. She’s just an egg producer. Complex behaviors like building the bridges you see on some websites2 emerge from interactions between individual ants following simple instruction sets without any designated leader.
Like ant colonies and termite colonies, humans consist of a collection of simple cells. Yet together, these cells achieve some amazing things!
Ant colony optimization techniques have been used in lots of businesses in recent years. Back in 1999, Air Liquide, in Texas, hired some Santa Fe Institute professors and they built an ant colony simulation system that saves them millions of dollars a year in distribution costs.3 Increasingly, companies outside of our industry are using ant colony optimizations, bee colony algorithms, and other modeling techniques based on the complex interactions of simple creatures to solve problems not soluble with our classic deterministic methods.
We might consider these nature-inspired methods. One of the ones most readily adaptable for actuaries in general, across all of our various specialties, is called genetic algorithms.
In the early 1970s, John Holland was a professor of computer science and of electrical engineering and of psychology at the University of Michigan, and he noted the astonishing level of complexity that has evolved in a relatively short period of time (viewed from the fossil record) and decided to mimic some of the processes used in natural evolution. His idea was to use the power of evolution to solve optimization problems. When I first started programming genetic algorithms, I kept drawing upon biology for inspiration whenever I ran into obstacles. My assumption was that if I learned more about genetics, I could be a better problem solver for genetic algorithms. After 10 semesters at Washington University’s mini medical school4, where I got to hold and inspect human brains, and lots of courses studying mitosis, meiosis, alleles, genotypes, phenotypes, single nucleotide polymorphisms and lots of other cool stuff I never did fully understand, I learned that to create genetic algorithms, you don’t need any of that! The term is just a metaphor. A fifth grader can understand genetic algorithms … and eventually, I did too.
In actuarial work, a genetic algorithm can help you find solutions to problems that might be difficult using conventional approaches. Let’s start with a contrived car trip example.
Example 1: This is a tiny example from an SOA presentation I gave, and you can view or download the entire presentation and the accompanying workbooks at https://github.com/DaveSnell/Genetic-Algorithms
Everyone has heard about the traveling salesperson problem. There are lots of techniques to solve it. Here is a version though with some unusual twists to it. Let’s assume you have potential clients to visit in eight cities. Some of these cities have more than one client in them; and some clients are more valuable, potentially, than others. If you want to meet with more than one in a particular city, you might have to make a return trip because of availability issues. In a normal traveling salesperson problem the number of solutions would be the number of cities as a factorial, but since we can visit any city more than once, we are looking at a solution set (for eight cities), of seven to the maximum number of interim trips, which I arbitrarily set to nine here, so we only have to choose between seven^nine or about 40 million routes.
Oh, but as GI actuaries know, the more miles you drive, the more you may be exposed to driving hazards. Let’s say that we don’t want to drive more than 1,000 miles. If a trip goes over 1,000 miles, I impose a mileage penalty of the amount of the overage.5 Since that is a big penalty relative to the points you can earn6, it is a conditioning item for our algorithm. How do we optimize this trip?
The best score you can get for a solution to this set of cities and weights is 16.75, which you can verify with the Excel solver if you wish. Excel’s solver add-in now includes an evolutionary solution option, which does not seem as fast as this one; but it works fairly well.
But, that was a simple, non-actuarial example. Now, let’s scale up to a tough insurance situation. You can find this in the workbook named Provider Network.
Example 2: Let’s start by Assuming that you have been asked to determine the makeup of a health insurance provider network. When Brian Grossmiller, my co-conspirator on this example first posed this problem, he had 7,000 potential provider groups, and each group had from one to 100 areas of specialty; but for this demo I am going to limit the example. Assume you have only 500 provider groups you may wish to include. Each of them has up to 36 different specialties, which may run the gamut from acupuncture, through obstetrics, oncology, all the way to X-ray technicians. You want to make available at least five urologists, at least 20 family practice doctors, etc. The minimum choice goals are empirical numbers you choose or are given as specifications. Some specialties, such as orthopedic surgeons tend to cost more than occupational therapists. Overall, some provider groups, perhaps those with more expensive specialties, or more expensive locations, will cost more than other provider groups. You want to minimize the overall cost.
We are making a simple assumption here that a provider group will be in the network, or not in it. That means, our number of possible set solutions is going to be two (in or out) to the 500th power, which is a little more than 10 to the 150th power. Let’s put that number into perspective. The number of atoms in the observable universe is estimated to be less than 10 to the 84th power. The number of seconds in time since the big bang origin of our universe is thought to be about 10 to the 17th power. If we multiply these numbers together, we get a very large number (of second-atoms?) that is still extremely small compared to the number of potential solutions to this problem.
But that’s not going to stop us because we are all familiar with mathematics, and pretty cool when it comes to solving numeric problems. Brian constructed his spreadsheet to normalize the provider group costs such that if every provider group were included, we would have a cost of 1.00.
Any consolidated number lower than one will be an improvement; and any result higher than one is more expensive.
Now, I’ve posed this problem to several very bright actuaries and with a few clever techniques they were able to reduce the cost to about 0.78 and at that point, they predicted that with enough time, they could get it down to 0.75 or perhaps even 0.70.
On a notebook PC with a very simple genetic algorithm I got the cost down to 0.70 in less than an hour. The notebook then continued to work away for another couple days without overtime, Red Bull, or potty breaks; and achieved 0.58.
Again, let’s put the numbers in perspective. If we are talking about a large health insurance network, a $300 machine can save 20 percent or more of potentially millions of dollars. It is pretty impressive.
So far, I talked about two examples and promised you that you can have copies of these workbooks7; but I haven’t showed you how this works yet. Very soon, we’ll learn to evolve; but first, let’s discuss when a genetic algorithm is a suitable technique for a mathematical problem.
Not every problem is suitable for a genetic algorithm. Let’s skip most of the biology and look at the criteria from a practical perspective. If you only have one variable, your genome is going to be pretty short and boring and there are better ways to solve your problem. If your problem involves a long string of variables it might be a natural for it. The human genome consists of a long string of over a billion pairs of A-T and C-G pairs. It seems to have been a good candidate.
But! You still have to be able to compare two solution sets and determine which is better. In nature, that might be a judgment of stronger, richer, smarter, more attractive. In a numeric problem it is usually whether your answer is larger or smaller.
Basically, I suggest that a genetic algorithm can be applicable when the following four criteria are satisfied:
- The problem involves a lot of variables—to some extent, the more there are, the better this technique applies.
- Each variable can take on potential values to produce different solutions.
- We can substitute a value for each of the variables, and that particular combination of individual values can be thought of as a solution set.
- The problem can be quantified in some manner so that any two solution sets can easily be compared to see which is better.
In the language of my grandkids, OMG can it be that simple? Do you mean the 10 semesters of mini-Med school were just for fun? Actually, they were fun; but you don’t need to replicate my journey into genetics to use so-called genetic algorithms.
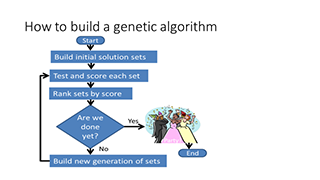
Figure 1- How to Build a Genetic Algorithm
Here is my overview of the process, in figure 1.
The initial solution sets can be completely random; or you can kick-start them with your special subject matter expertise. I find that on really complex problems, that for generation number one, my subject matter expertise sometimes gets in the way, so I like to start with a random collection (we call that a generation) of solution sets.
Your workbook, or program or whatever, has to be able to try each of these sets, and to score them. That’s where much of the subject matter expertise is useful.
Once you have tried and scored every set in the generation, rank them by score. If the best score meets your acceptance criteria, you are done.
If that happened on the first generation then maybe this problem was not such a great genetic algorithm application after all. It was too easy. But if it doesn’t meet the acceptance criteria, let’s build a new generation of sets and try again, continuing the process.
But wait! This sounds like trial and error. Where is the genetic part?
Good question! It’s mostly in that lower box of figure 1. The one that says, “Build new generation of sets.”
We don’t want to keep using trial and error like we essentially did in generation one. We want to take advantage of what we learned in that previous generation.
One thing we learned is that some solution sets did a lot better than other ones. We’ll keep the top performers and bring them intact into the next generation. That way, the next generation cannot turn out dumber or less suitable than the previous one. As mathematicians, we are guarantying the solution is monotonically improving. These top performers have earned what we call elite status. The non-elites die off and are replaced by the new children; but these hardy individuals live on for at least another generation. Let’s look at some sample code and see how that is done.
Assume that we chose to have 100 solution sets in each generation. And, let’s assume that we want the top 20 (the 20 best scoring ones) to be the elites. In less than a dozen lines, we can write the code to create the children of the next generation.
Note that in line #4, I am going to step far away from biology here because I have a chance to improve my algorithm’s learning rate by changing the rules. I am going to allow more than two parents for each child. When I first started with genetic algorithms I thought that was heresy. Ben Wadsley and I were solving an asset/liability management (ALM) problem with genetic algorithms and he got faster results by drawing from five parent sets. Now, I designate some large percent of my generation, say 40 out of the 100, to be the parent pool, and I draw from that pool for each variable in my next generation of solution sets.
If you want, you can set the number of potential parents to the entire set of elites or just a portion of them, or even go beyond them. Our parent pool can be smaller, equal to, or larger than the number of elites. Let’s assume here that parentPool = 40.
Note that another step, which I don’t show here because the figure is already busy, is to sprinkle in some mutations. Don’t mutate an elite; but as your generations progress, mutations become more useful to temper inbreeding. Among humans, there are often laws against inbreeding. It can result in very unhealthy children who lack genomic diversity and that makes them vulnerable to diseases that the rest of the population can survive. Inbreeding is also very bad for genetic algorithms.
In order to help you get started with genetic algorithms, the training workbook I created lets you experiment with different numbers or elites, parents, mutations, scoring objectives, and other parameters so you can use these to solve problems without ever having to write any programming code. The source code is also easily viewed so that if you wish you can inspect it or modify it.
I maintain that genetic algorithms can be a lot easier to learn than algebra was. Plus, I would say that billions of years of evolution has validated it pretty well! But is it cool and useful in this new age of predictive analytics and neural networks. Don’t they eliminate the need for this? Another colleague of mine, who is a non-actuary, just combined genetic programming and deep neural networks in his March, 2017 Ph.D. thesis.8 The combination of very old, and very new techniques working together can be very powerful!
Evolutionary algorithms are merely the tip of the iceberg of complexity techniques. If you liked reading and learning about them, please let me know. Better yet, read the excellent research paper by Alan Mills, Complexity Science – An Introduction (and Invitation) for Actuaries.9 The Health Section published this in June of 2010 and it stands as a pioneering opus for actuaries who want to know more about complexity sciences. I find deterministic chaos, fuzzy logic, behavioral economics, cellular automata, agent-based modeling, fractal analysis, and lots of other complexity sciences fascinating; and I look forward to the opportunity of sharing my enthusiasm for them. Come out from under your rock. Enjoy this complex and wonderful world!
Dave Snell, ASA, MAAA, is technology evangelist at SnellActuarialConsulting in Chesterfield, Mo. He can be reached at dsnell@ActuariesAndTechnology.com.
1"I can't define pornography … but I know it when I see it.”- Justice Stewart in Jacobellis v. Ohio 378 US 184 (1964).
2 http://www.undergrowth.org/ant_bridge
3Evolutionary Computation at American Air Liquide, by Charles Neely Harper, Lawrence Davis in chapter 15 of Evolutionary Computation in Practice, 2008, Editors: Associate Professor Tina Yu, President Lawrence Davis, Director Cem Baydar, Professor Rajkumar Roy ISBN: 978-3-540-75770-2, Springer
5On the Sales Trip tab of the GA Training Tool workbook, you can see that in cell F27.
6On the Sales Trip tab of the GA Training Tool workbook the points you can earn are shown in cell F26
7All the workbooks and the related slides are available at https://github.com/DaveSnell/Genetic-Algorithms
8“Automated Feature Engineering for Deep Neural Networks with Genetic Programming”, by Jeff Heaton, A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Computer Science, College of Engineering and Computing, Nova Southeastern University, 2017, ProQuest Number:10259604
9 /Search.aspx?q=complexity+science+-+an+introduction+and+invitation
