by Shea Parkes and Brad Armstrong
This article first appeared in the July 2015 issue of Forecasting & Futurism. It is reprinted here with permission.
Risk adjustment models are commonly used in managed care programs to ensure that participating health plans are compensated based on their ability to manage costs, rather than on the underlying morbidity of their enrollees. The accuracy of the models can influence which plans receive a larger (or smaller) proportion of the funds.
A variety of claims-based risk adjustment models are available; each is designed to predict costs for a certain type of program, such as a Medicaid population versus a commercial population. However, the variety of managed care populations (and benefits) is much larger than the variety of off-the-shelf risk adjustment models that are available. It is inevitable that any specific program will exhibit characteristics – reimbursement, covered benefits, prevalence, and severity of disease states - that are different from those assumed by even the most appropriate model available. For example, a common concern in Medicaid is that reimbursement varies materially between states. The target program may have higher hospital reimbursement and lower professional reimbursement than other programs, or vice versa.
Although the off-the-shelf model may still do an acceptable job of predicting costs, it is likely that the accuracy of the model could be improved by recalibrating it to better fit the specific population for which it is being used. Most risk adjustment models are based on linear regression, so a common method of adjusting the model is to estimate new parameters (or weights) for the population of interest.
However, estimating new weights is only appropriate if the population is large enough to provide credible estimates of all the potential coefficients, especially those associated with less prevalent conditions or disease states. For example, the population may be large enough to support adjustments for more common conditions such as diabetes, but adjustments for less common conditions, such as tuberculosis or rare genetic conditions, may be based on a small sample of a few individuals and not fully credible. The off-the-shelf models represent valuable learnings from a very large, very credible data source. Instead of estimating completely new weights, it is possible to use a technique known as ridge regression to only adjust the coefficients that are credibly different for the target population. This can result in a model that is better than either of the off-the-shelf coefficients, or a one that is completely retrained on the target population.
Definitions of “better” are often nebulous, especially when dealing with concurrent risk scores. In this case, “better” means that the model produces a lower error metric on a new dataset (other than that used to train it). If “better” were instead focused on the lowest error metric on the dataset used to train the model, then the fully re-estimated model will be best as long as it is optimizing the corresponding loss function. In the following example, the new dataset used to judge performance was claim experience from a different year of the program for the same population used to re-estimate the model.
An applied example
Recently, we have been exploring different techniques to recalibrate the Medicaid Rx (MRx) model to better fit specific populations. Medicaid Rx, a risk adjustment model designed for Medicaid populations, uses enrollment and National Drug Code (NDC)-coded pharmacy claim data to assign individuals to age and gender categories and to flag each member for the presence of a variety of medical conditions, which are identified based on pharmacy utilization. The age/gender buckets and condition flags are then used as features in a linear regression model that predicts a risk score for each member. While we wanted to keep the variables used in the standard Medicaid Rx model intact, our goal was to reweight these variables in the linear model to better fit the characteristics of specific Medicaid programs and to improve the accuracy of the predictions on new data.
With enough data and experience, one way to accomplish this would be simply to take the known normalized costs of individuals, and fit a new linear regression model with the same features as the standard MRx model in order to completely recreate the coefficients from scratch. However, some populations are not large enough to be considered fully credible on their own. In this example, we focused on a population with approximately 30,000 members, which is not large enough to warrant full credibility. Instead of completely retraining the MRx model, we used the standard MRx weights as a starting point, but made adjustments to the coefficients of the model based on evidence from the population data. To strike this balance, we used a penalized regression and cross validation to choose a reasonable point between the standard weights and completely retrained weights.
Our linear regression model for creating new weights included all of the features of the standard MRx model (the demographic and condition variables), but also included an additional “offset” variable that represented the original model’s risk score prediction. In a standard linear regression with conditional Gaussian response, this is equivalent to fitting a new model on the residuals of the original model. However, the “offset” paradigm can still apply in a generalized linear model setting.
Adding this new variable effectively meant that the coefficients estimated for all of the other features in the model could be interpreted as “deltas,” or the adjustments that should be made to the standard/original weights. We then estimated the delta-coefficients with a ridge regression penalty, optimized via cross-fold validation. The ridge regression penalizes a model for the sum of its squared coefficients; this tends to prefer models with smaller coefficients versus those with wildly large coefficients even if the latter are slightly more accurate on the training data set. Because the coefficients were in fact “deltas” from the original coefficients, this essentially favors models that are closer to the off-the-shelf model. An alternative interpretation is that we put strong Bayesian priors on each coefficient, centered at the values used in the standard MRx model. Because the ridge regression framework adds a larger penalty as the coefficients for each variable get further away from zero, the tendency of the model was to use values close to the standard weights unless there was strong evidence in the population data that a certain coefficient should be changed. Even better, since the size of the ridge penalty can be scaled using a parameter, we are able to tune the procedure to vary the amount of credibility given to the population data.
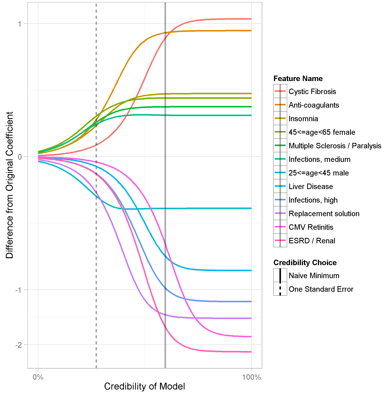
Figure 1 shows how the values of the coefficients for select features change as different levels of credibility are given to target population data.
Figure 1: Values of Coefficients for Select Features
The outcome variable of our regression model was the normalized cost of each individual. The outcomes for very high cost individuals were capped at the 99.5th percentile cost of the population. This was done to avoid having a handful of observations inordinately affect the values of the coefficients estimated by the regression model. For example, one very high-cost individual flagged for a certain condition could singlehandedly push the coefficient associated with that condition much higher than it should be. By introducing the cap to the outcome variable, that individual would still be considered high-cost in the regression, but not by several orders of magnitude, which could swamp the importance of all other observations with that condition. This was especially important for the process of cross validation explained below.
To perform the ridge regression with cross validation, we used the glmnet package in R, which allows the user to fit a regression model with a ridge penalty, a lasso penalty, or a blend between the two (elastic net penalty). A lasso model penalizes the sum of the absolute values of the coefficients, while the ridge model penalizes the sum of the squared coefficients. By using the ridge penalty, the regression produced non-zero delta-coefficients for all of the features in the model, but the size of the adjustment varied based on the evidence in the population data. Using a lasso penalty would have made the delta-coefficient for many of the features zero, while only making adjustments to coefficients for which there was strong evidence. While the lasso approach could also produce reasonable results, we chose ridge regression based on a prior assumption that none of the coefficients were precisely centered for the target population.
Choosing a specific set of coefficients
To decide how strong a ridge penalty to apply, we utilized 10-fold cross-validation within the training data. This means the training observations were divided into 10 segments, and the regression was performed 10 times, leaving a segment of the data out each time. For each fit, the model was judged against this smaller portion of the training data that was currently withheld, generating a cross-validated error metric. In theory, this produces a more realistic estimate of model performance on new data. There is still uncertainty about how new data might differ from the training data, so even this estimate of accuracy should be used with caution. For this application we utilized root-mean-square-error as the error metric, after capping high extremely cost members’ outcomes to bound their influence. The insights should be the same for any reasonable choice of error metric.
This whole cross-validation procedure was repeated for different sizes of ridge penalty to produce a range of generalization error estimates for different penalty sizes. Instead of picking the penalty value with the absolute best cross-validated error estimate, we chose a slightly simpler (closer to off-the-shelf) model that was within one standard error of the minimum cross-validated error estimate. This is a standard convention to protect against overfitting, because resampling the training data does not truly reflect the new data to which one might want to generalize.
Figure 2 displays the error estimate for a range of penalty values. For our final model, we chose to use a penalty value for which the error estimate was within one standard error of the minimum, in order to prevent overfitting to new data.
Figure 2: Error Estimates for Penalty Values
In this example, our goal was to generalize to the next year of claims. Upon actual application, it was shown that the penalized model produced a better average error metric on the new year of data than the off-the-shelf model, and one very similar to the fully re-trained model. The specific error metrics are presented in the table below:
| Model Description | Error Metric on Next Year of Claims |
| Off-The-Shelf | 3.157 |
| Partial Credibility | 3.123 |
| Fully Re-trained | 3.123 |
While the penalized model exhibited the same level of predictive power as the fully re-trained model, the coefficients used in the penalized model appeared more reasonable and credible, because the weights for certain features were not based entirely on a low volume of observations. Using this methodology allowed us to still use the information contained in the standard weights of the MRx model, but to adjust them slightly to better accommodate the characteristics of this specific program. We recommend exploring this approach when trying to recalibrate a model for a population that is of a moderate size, but perhaps not fully credible.
References
Department of Family and Preventive Medicine, University of California, San Diego. Medicaid Rx. http://medicaidrx.ucsd.edu/
H. Wickham. ggplot2: elegant graphics for data analysis. Springer New York, 2009.
Jerome Friedman, Trevor Hastie, Robert Tibshirani (2010). Regularization Paths for Generalized Linear Models via Coordinate Descent. Journal of Statistical Software, 33(1), 1-22.
R Core Team (2014). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.
Trevor Hastie, Robert Tibshirani, Jerome Friedman. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition. Springer Science & Business Media, 2009.
Shea Parkes, FSA, MAAA, is an actuary at Milliman in Indianapolis. He can be reached at shea.parkes@milliman.com.
Brad Armstrong, FSA, MAAA, is an associate actuary at Milliman in Indianapolis. He can be reached at brad.armstrong@milliman.com.
.png)