Quantum Actuarial: Part 2—The Prelude of the Harmonic Oscillator

Part 1 of this article discussed the innovative application of the quantum harmonic oscillator model in actuarial science. We explored how the probabilistic wave distribution characteristics of the quantum harmonic oscillator, as described by the Schrödinger equation, provide insights into medical cost distribution and interest rate fluctuations in insurance pricing and assessment.
In this part of the article, we will delve deeper into the complexities introduced by external influences, extending our discussion to the quantum anharmonic oscillator model. We will analyze how different types of external forces—constant, linear, and nonlinear—affect the probability distribution functions, drawing parallels with the external factors influencing medical costs and interest rates in the insurance industry.
External Influences—Quantum Anharmonic Oscillator Model
The ground state probability distribution of the quantum harmonic oscillator is a standard normal distribution. However, in the real physical world, almost no systems are completely isolated. External forces or potential function disturbances often disrupt this idealized equilibrium, causing the probability distribution of the quantum harmonic oscillator to deviate, exhibiting more complex and variable characteristics. When external forces are introduced, the dynamic behavior of the harmonic oscillator is no longer limited to its inherent frequency and amplitude. These forces may come from various physical processes, such as the action of electromagnetic fields, interactions between particles, etc. They affect the motion state of the harmonic oscillator in different ways and intensities, leading to significant changes in its probability distribution. These changes are not only reflected in the shape of the distribution but may also be manifested in statistical features such as the width and peak of the distribution.
Drawing an analogy between this physical phenomenon and the medical costs and interest rate patterns in insurance pricing, many similarities can be found. Just as the quantum harmonic oscillator is disturbed by external forces, medical costs are also affected by various external factors, such as disease incidence rates, advancements in treatment technology, and the allocation of medical resources. Fluctuations in interest rates are also influenced by a variety of factors, including but not limited to economic cycles, monetary policy, inflation rates, market supply and demand, and international factors. Changes in these factors can cause fluctuations in medical costs and interest rate levels, thereby affecting their normal distribution in the base state. This phenomenon of deviation from the normal distribution also needs attention in insurance pricing and assessment.
The external forces affecting medical costs and interest rate levels can be expressed by the following formula:
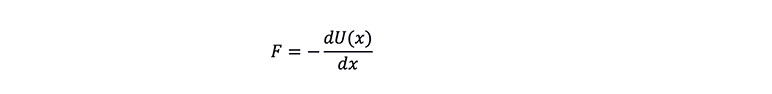
where U(x) is the external potential function. In insurance actuarial terms, the external force describes any local or individual behavior that causes the distribution of medical costs and interest rate levels to deviate from the equilibrium state; while potential energy is the global effect caused by these local or individual behaviors, reflecting the overall operation status and trends of the external environment. Substituting it into the Schrödinger equation:
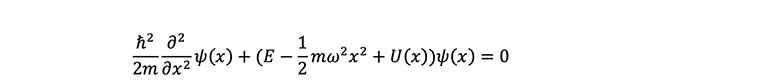
When the external force F = 0, the Schrödinger equation will revert to the standard quantum harmonic oscillator equation, and its ground state solution is the standard normal distribution. Next, we will explore the effects of different force on the probability distribution of the quantum harmonic oscillator and draw an analogy to the situation of insurance pricing and assessment, hoping to gain some insightful thinking.
Constant External Force
When the external force is a constant force, it is equivalent to applying a fixed offset to all medical costs or interest rate levels. That is, when F=-a and
U(x)=ax, the Schrödinger equation can be expressed as:
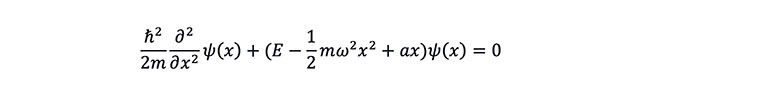
By solving the partial differential equation, its ground state solution can be represented as:
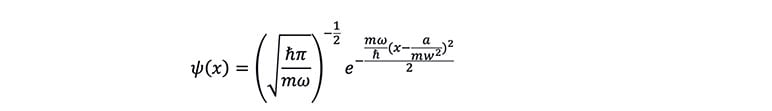
It can be seen that the expression for ![]()
is a normal distribution function with its peak shifted to
![]() , indicating that the effect of the constant external force will cause the central peak of the standard distribution function to shift, but it will not affect its volatility. When
, indicating that the effect of the constant external force will cause the central peak of the standard distribution function to shift, but it will not affect its volatility. When ![]()
, it means that the influence of the external force will reduce medical costs, shifting the peak to the left, and vice versa. (See Figure 1)
Figure 1
The Impact of Constant Force on the Probability Function
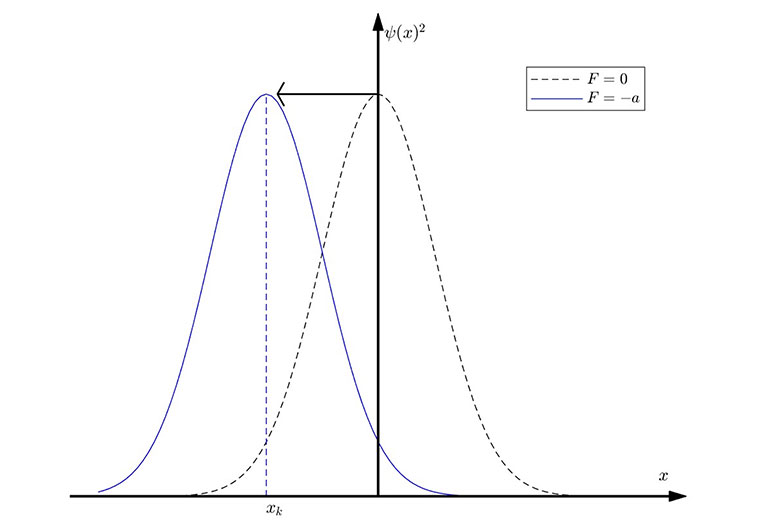
Taking medical insurance as an example, the impact of inflation on the cost of medical insurance can be regarded as a disturbance by a constant force. When considering the robustness of the medical security system, the dynamic changes in the medical insurance claims cost undoubtedly occupy a central position. In recent years, the annual increase in claims costs has become an undeniable fact, a trend largely attributable to the general rise in medical expenses and the devaluation of currency, both of which are direct products of the inflation effect. In light of this, insurance companies will face increasing claims expenditures to ensure insureds receive the necessary medical services, which essentially puts additional pressure on the insurance companies.
According to an analysis of the cost trend of a commercial health insurance product in China, an interesting phenomenon can be observed. As shown in Figure 2, from 2018 to 2022, medical insurance claims costs have shown an increasing trend each year, but at the same time, the fluctuation of the distribution of claims costs has remained relatively stable. This phenomenon indicates that the universal increase in claims costs due to inflation is similar to the central peak shift while the variance remains constant when a quantum simple harmonic oscillator is subjected to the action of a constant external force. It profoundly reveals the universality and uniformity of the impact of inflation on medical insurance claims costs. This means that although each claim case receives an increased amount due to inflation, the extent of these increases is relatively consistent across different cases. Inflation has a uniform impact on the claim amounts of all insureds, rather than selectively affecting certain specific groups. This result provides an empirical basis for an in-depth analysis of the impact of inflation on medical insurance claims, and the action of a constant external force on a quantum simple harmonic oscillator.
Figure 2
Box Plot of Medical Costs Under a Commercial Health Insurance Product in China
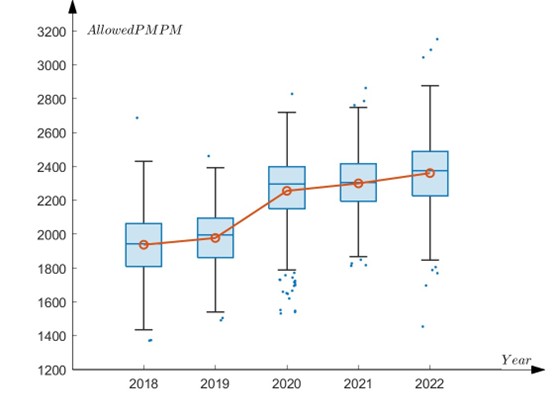
Regardless of the specific circumstances of the insureds, the degree of impact of inflation on their claim amounts is consistent. This consistency is of great significance for insurance companies when setting insurance rates and claim strategies, as it helps them to predict claim costs more accurately, thereby providing reasonable insurance coverage for insureds while maintaining financial stability. At the same time, it also suggests that policymakers need to consider the universal impact of inflation on medical costs and insurance claims when considering medical subsidies or insurance policy adjustments, to ensure the effectiveness and fairness of policies. Using the quantum oscillator model for analogical analysis, the mathematical principles reflected by the model, that is, the changes in the system's energy distribution under the action of external forces, can provide us with a powerful tool to understand and predict the dynamic changes in medical insurance claim costs.
Linear External Force
If the external force is a force that has a linear relationship with medical costs, that is, ![]()
, the Schrödinger equation can be expressed as:
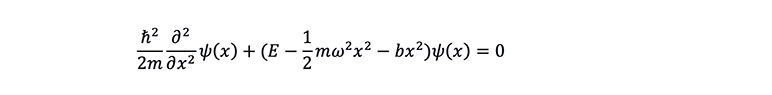
By solving the partial differential equation, its ground state solution can be represented as:
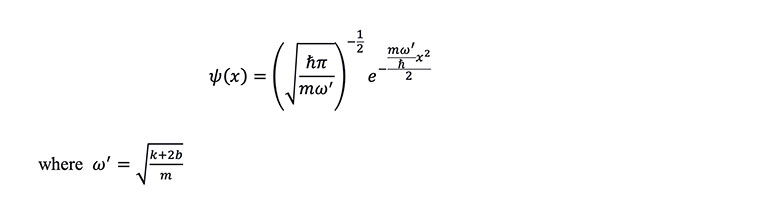
It can be seen that the expression for ![]()
is a normal distribution function with the peak position unchanged and the volatility changed, indicating that the linear force will affect the dispersion of medical costs. (See Figure 3)
Figure 3
The Impact of Linear External Forces on the Probability Function
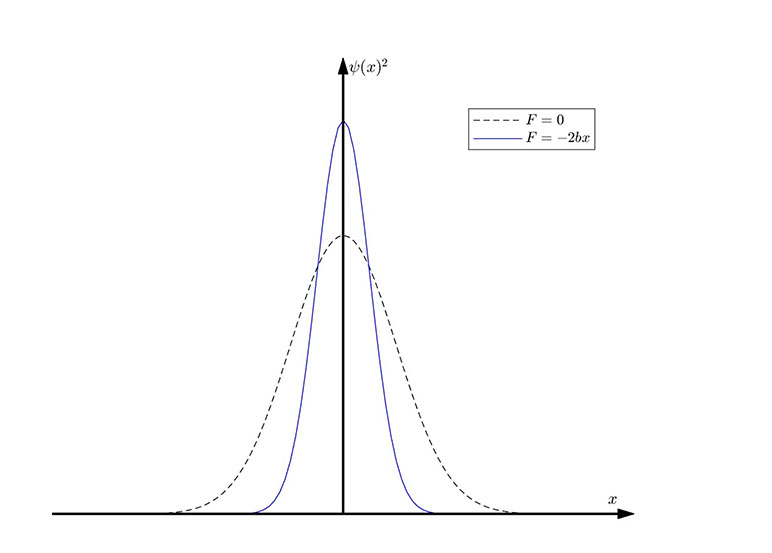
In the field of actuarial science, surplus reinsurance can be considered as an example of a quantum simple harmonic oscillator model under the influence of a linear force. Surplus reinsurance is a form of proportional reinsurance that allows the original insurance company to transfer the risk exceeding its retention limit to the reinsurer. In a surplus reinsurance contract, the original insurance company sets a fixed retention limit, and the insurance amount exceeding this limit is shared with the reinsurer according to a certain proportion. This arrangement helps the original insurance company to expand its underwriting capacity and to diversify risks in the face of large-scale payouts.
Mathematically, for a normally distributed random variable X, as the constant
T increases, the distribution of min(X,T)
will approach the distribution of X
. Moreover,
![]() , suggesting that
, suggesting that E[min(X,T)] converges to E[(X)] much faster than
![]() convergence to
convergence to ![]()
. If we consider X
as the insurance risk and
T as the retention limit, then min(X,T)
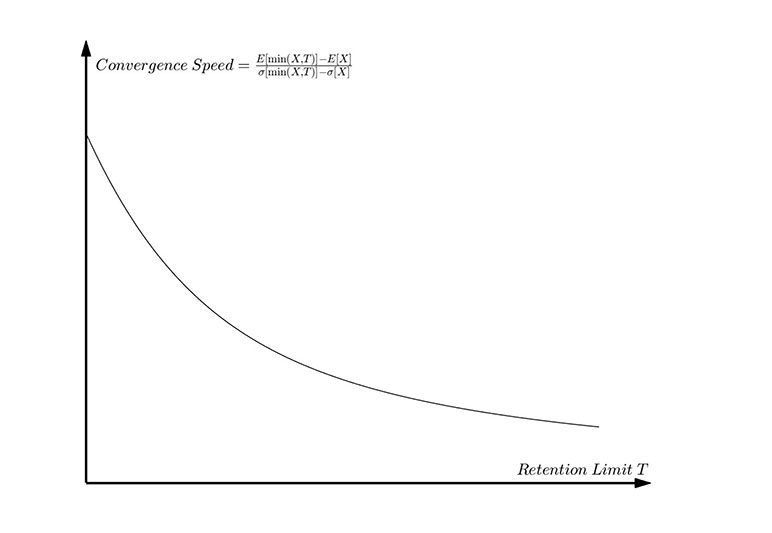
can be regarded as the retained risk after surplus reinsurance. As the retention limit increases, the convergence rate of the expected value of the retained risk distribution is much faster than that of its standard deviation, as shown in Figure 4. When the retention limit T is sufficiently large, the retained risk min(X,T)
of the insurance company can be regarded as a distribution with an approximately constant expectation but a different variance. This proves that surplus reinsurance can be approximated as a quantum harmonic oscillator model under a linear force.
Figure 4
Surplus Reinsurance Retention and Convergence Speed
Generally speaking, the purpose of reinsurance is to mitigate extreme risks, hence the retention limit is significantly higher than the expected payout of the insurance. This mechanism indicates that the average payout for the insurance company only changes slightly and remains essentially unchanged. However, large claims that exceed the retention limit will be borne by the reinsurer. It can effectively reduce the risk of great fluctuations in the payout costs caused by a few extreme events for the original insurance company, thereby significantly reducing the volatility of the payout costs, as shown in Figure 5.
Figure 5
The Impact of Surplus Reinsurance on Claim Costs
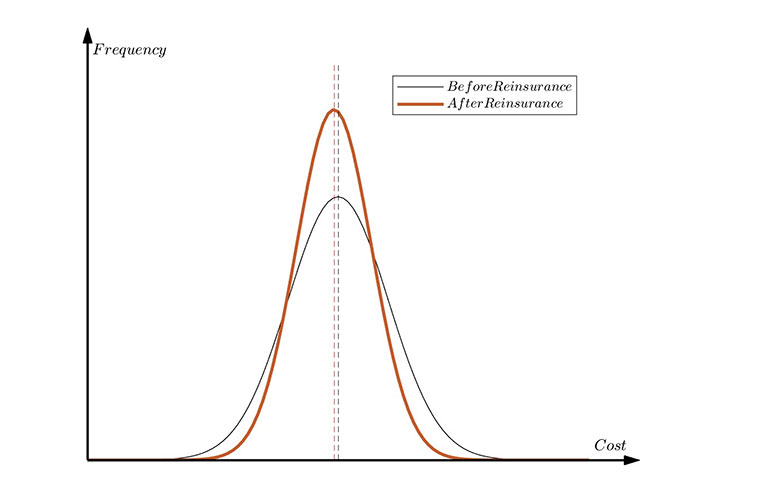
Therefore, the surplus reinsurance helps enhance the stability of claim costs with an approximately unchanged claim cost, yet a reduced variance. This corresponds to the characteristic in the quantum harmonic oscillator model under linear force, where the peak position remains unchanged while the volatility decreases. The quantum harmonic oscillator model under linear force can provide an effective risk management framework and assessment tool for surplus reinsurance strategies. However, if the retention limit is set too low, resulting in a significant decrease in both the average claim costs and volatility, then a more precise risk assessment and optimization of management strategies can be further applied using the composite quantum harmonic oscillator model with constant force and linear external force.
Nonlinear External Force
When the external force is nonlinear, it becomes more challenging to obtain direct analytical solutions. Taking a quadratic external force as an example, that is ![]()
, the Schrödinger equation can be expressed as:
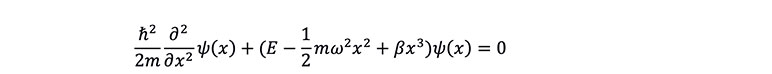
Since the potential energy contains a cubic term, solving the Schrödinger equation directly by analytical methods is quite challenging. Variational methods are required to approximate the ground state wave function, and the optimal parameters are found by minimizing the energy functional, thereby estimating the ground state energy. The probability distribution function of the ground state is no longer a simple normal distribution but exhibits a more complex pattern, as shown in Figure 6.
Figure 6
The Impact of Quadratic External Force on the Probability Distribution Function
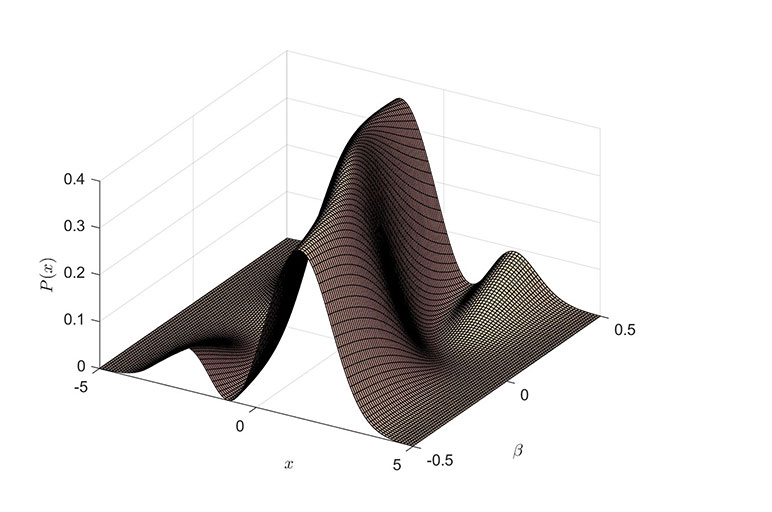
When the external force is nonlinear, it implies that the external influencing factors have a nonlinear growth characteristic, making the corresponding scenarios more complex. Specifically, in terms of medical insurance, many factors have a nonlinear relationship with medical costs. For instance, research indicates that there is a nonlinear relationship between Body Mass Index (BMI) and medical costs[1] (Laxy et al., 2017). As BMI increases, medical costs exhibit a trend of initially slow increase followed by a rapid rise. Particularly when BMI reaches obesity class III (BMI ≥ 40 kg/m²), the rate of increase in medical costs further accelerates. This nonlinear relationship can be simulated using the probability distribution in the quantum harmonic oscillator model under the influence of a nonlinear external force. Although the quantum harmonic oscillator model under the influence of a nonlinear external force is relatively complex and the specific mathematical model is difficult to solve analytically, its impact on the system can be estimated through numerical methods such as variational methods. Drawing on the quantum harmonic oscillator model under nonlinear external forces, we can better understand and address the impact of various nonlinear factors on medical costs, providing new ideas and methods for precise pricing.
By drawing an analogy to the quantum simple harmonic oscillator being influenced by external forces, we can better understand the causes and impacts of medical costs and interest rate fluctuations in insurance actuarial work. This helps insurance companies to more accurately assess risks, formulate premium strategies, and make wiser decisions in risk management and resource allocation. At the same time, it also reminds us that in the insurance market, it is necessary to pay close attention to the changes in various external factors in order to adjust pricing and assessment strategies in a timely manner to cope with potential market risks. Future research can further explore the effectiveness of these models in practical applications and consider more types of external forces and their impact on the quantum simple harmonic oscillator.
Conclusion
This article explores the application of the quantum simple harmonic oscillator model in actuarial science, demonstrating how this model provides a new perspective for understanding risk assessment and cost distribution in actuarial practice. By analyzing the probability wave properties of the harmonic oscillator, the article reveals the correlation between these properties and the distribution of medical costs and interest rate patterns in actuarial practice. This can help in understanding the multimodal characteristics of medical cost distribution and the intrinsic mechanisms of interest rate fluctuations. In the section on external forces, the article discusses how the probability distribution changes when the quantum simple harmonic oscillator is subjected to different types of external forces, and draws an analogy to medical cost and interest rate fluctuations in actuarial science. This can assist insurance companies in more accurately assessing risks, setting premium strategies, and making wiser decisions in risk management and resource allocation.
Future research can further expand the application scope of the quantum simple harmonic oscillator model in actuarial science. This article is limited to the one-dimensional harmonic oscillator model, while the risks faced by insurance companies are often multidimensional. Therefore, exploring multidimensional quantum simple harmonic oscillator models is essential for a more comprehensive assessment and management of these risks. Moreover, practical case studies can be used to verify the effectiveness of the model and optimize its application. Future research can also consider more types of external forces and their impact on the quantum simple harmonic oscillator, as well as how to use these models to develop more effective risk management strategies. With the deepening of interdisciplinary cooperation, the quantum simple harmonic oscillator model is expected to bring more innovative ideas and technological breakthroughs to the field of actuarial science.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.
Endnote
[1] Laxy, M., Stark, R., Peters, A., Hauner, H., Holle, R., & Teuner, C. M. The Non-Linear Relationship between BMI and Health Care Costs and the Resulting Cost Fraction Attributable to Obesity. International Journal of Environmental Research and Public Health (2017)
