Optimizing Open System Actuarial Models

Open system actuarial models offer significant flexibility, allowing users to customize calculations to meet their specific needs. However, this flexibility can lead to inefficiencies if models are not properly optimized. Given this risk, this article highlights methods for optimizing open system models, a skill often associated with computer scientists rather than actuaries. Optimized models run more efficiently and reduce downtime, which can translate to cost savings. Faster runtimes can also enable additional analysis, allowing management to make faster and more informed decisions.

Introduction to Open System Actuarial Models

Open system models are platforms that allow users to modify underlying structure and calculations, offering significant flexibility. In contrast, closed system models have fixed structures and calculations that cannot be altered by the user. Table 1 compares additional key differences between open system and closed system models. While we use a binary distinction between open and closed systems throughout this article, it is important to recognize that most modeling platforms fall somewhere between the open and closed spectrum.

Table 1
Open versus Closed System Comparison

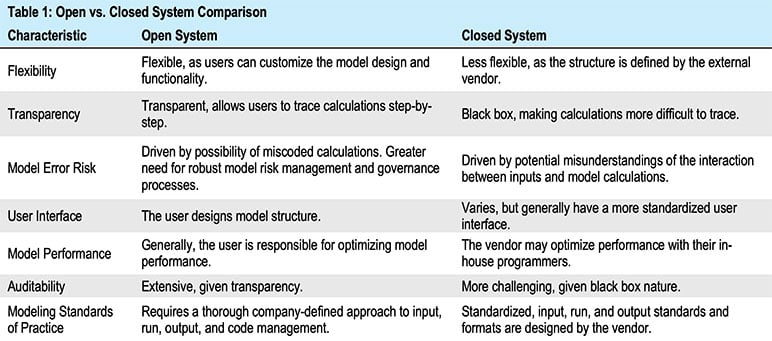
There are tradeoffs between open systems and closed systems. Closed systems generally provide stability because the user cannot substantially change the functionality. However, this stability is at the cost of loss of flexibility. Certain product types or specific company needs may require a degree of flexibility/customization to be properly modeled. Open systems provide greater transparency and allow users to customize calculations, but this can increase model error risk without thoughtful governance processes.

Framework for Optimizing Model Performance

As shown in Table 1 above, open systems give users responsibility for optimizing model performance. Alternatively, the external vendor is generally responsible for model performance optimization for closed systems. Given this distinction, it is not only prudent, but necessary, for open system users to consider model performance when developing their models.

Below is a framework (inspired by the Actuarial Control Cycle) for improving model performance:

• Identify inefficiencies: Before improving efficiency, a user should first identify the areas where their model is inefficient. As an example, some platforms contain diagnostics allowing a user to determine the time spent by each calculation.
• Implement like a computer scientist: After the problems have been identified, it becomes time to implement solutions. However, an actuary must put on their computer scientist hat. We recommend eliminating redundant calculations and reducing reliance on computationally expensive calculations. While not historically associated with actuaries, runtime optimization should be a consideration for open system model users.
• Test and evaluate the solutions: After executing, the optimized model must now be tested before going into production. One needs to test that a) the model now performs better, likely measured as change in runtime, and b) the model still produces the same results. Adjusting runtime should not change underlying calculations, generally.i
• Monitor the performance: Once a model has been optimized, users should continue to monitor performance to avoid recurrent model bottlenecks that reduce efficiency. In our experience, we have seen coding updates which inadvertently increased runtime.

Methods for Optimizing Model Performance

This section presents specific methods for reducing runtime and improving model performance using the steps presented in Table 2 below. Color coding in Table 2 is linked to the case study presented in the section below.

Table 2
Examples of Optimization Methods

Below is more detail on the methods presented in Table 2.

• Loop Design: Loops require iteration and can be computationally intensive, especially “nested for loops” (loops within loops). Modelers should ensure that the boundaries of the loops do not lead to unnecessary calculations. Further, it may be prudent to move certain calculations outside of the inner loop.
• Application: Multi-state models (e.g., disability insurance, long-term care insurance, and deferred lives in pension risk transfers) may require many looping calculations.
• Frequency of “table-reads”: The process of reading tables is computationally intensive because the computer must retrieve the necessary table values each time a table read function is called. This can increase runtime dramatically if table-reads are called within inner loops.
• Application: Code optimization where table-reads are moved outside of an inner loop. See Case Study’s Step 2 in the next section for a specific visual example.
• Parameterized Calculations: A parameterized calculation is programmed once and can be re-used throughout the model based on parameters. Parameterized calculations provide several benefits to open system models, including minimizing code and programming efforts as well as easing auditability by storing the code in one location. While this method may or may not improve runtime, we have included this method since parameterized calculations can improve coding efficiency and reduce model error risk.
• Application(s): User defined functions, multi-state modeling, and combining models to perform several functions (e.g., valuation and pricing).
• Recursion: Recursive functions call themselves and allow users to use the prior (or subsequent) value of the recursive function. This prevents prior (or subsequent) values from being re-calculated multiple times.
• Application: Frequently used items in projections such as policy duration.
• Non-Repeating Calculations: Some calculations only need to be calculated once per model run or once per model cell. In essence, models should avoid performing the same calculation multiple times.
• Application: Reading a scenario file once at the beginning of the model run instead of for each cell.
• Closed Form Solutions: Closed form solutions may be less calculation intensive than iterative solving algorithms.
• Application: Premium solving for universal life XXX reserves.
• Distributed Processing: Distributed processing allows users to run the model on multiple computers simultaneously, lowering the aggregate runtime.
• Application: Multiple interest rate scenarios for interest sensitive liabilities such as year-end cash flow testing.

Model Optimization Case Study

To highlight some of the methods presented, we present an illustrative case study of a disability insurance model. Disability insurance requires multi-state modeling. A policy starts in the active state and may subsequently transition (incidence rate) to the disabled state.ii For each disability date, the model must project disability payments by duration based on claim continuance (probability a disabled life stays on claim).

In this case study, the model needs to project future disability benefits for a cell in the active state given it can move into the disabled state at a given age. Figure 1 below is the initial design for claim termination rates, or the probability that a disabled life ceases receiving disability benefits.

Figure 1
Claim Termination Rates—Initial Design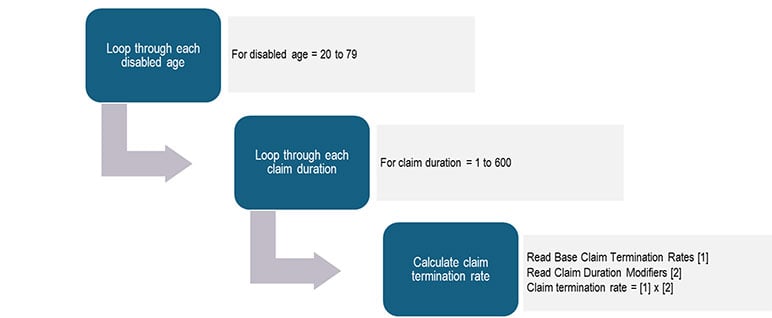

The runtime is stressed from overextended loop boundaries and reading tables excessively. We iteratively improve this illustrative disability model in three steps:

• Step 1: Loop Design
• Step 2: Reading Tables
• Step 3: Parameterized Calculations

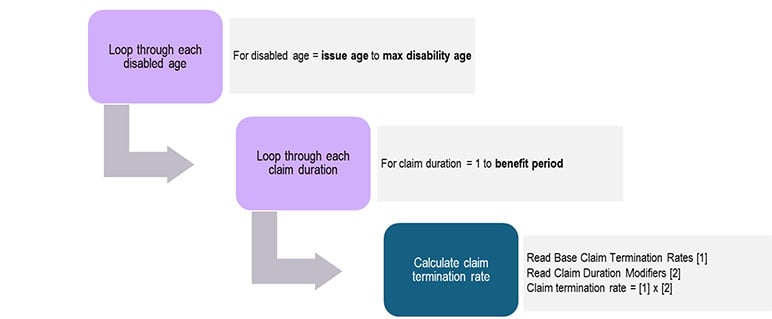
Step 1: Figure 2 reduces the loop boundaries which will reduce runtime significantly. Rather than setting the initial and ending ages as a deterministic value, by changing to using issue age and max disability age, the loop will only be performed for the minimum amount of times. For example, an issue age 35, benefit period to 65 years cell, this optimization reduces the loop size by 85%.iii

Figure 2
Claim Termination Rates—Loop Optimization

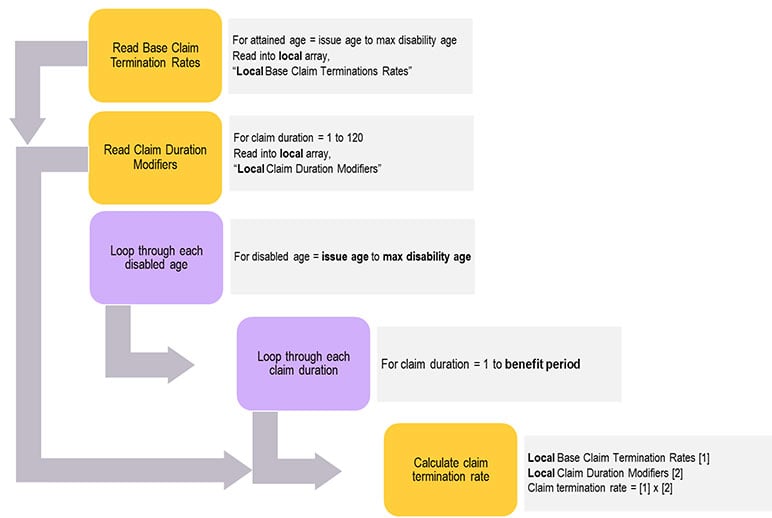
Step 2: Figure 3 appears more complicated than Figure 2. However, it will reduce runtime as it reads tables outside of the inner loop and leverages local arrays. Applying this change could reduce the number of table-reads steps by well over 90%. Limiting the reading of tables has broad optimization applications because most, if not all, actuarial models rely on some degree of assumption tables.

Figure 3
Claim Termination Rates—Reducing Table Reads

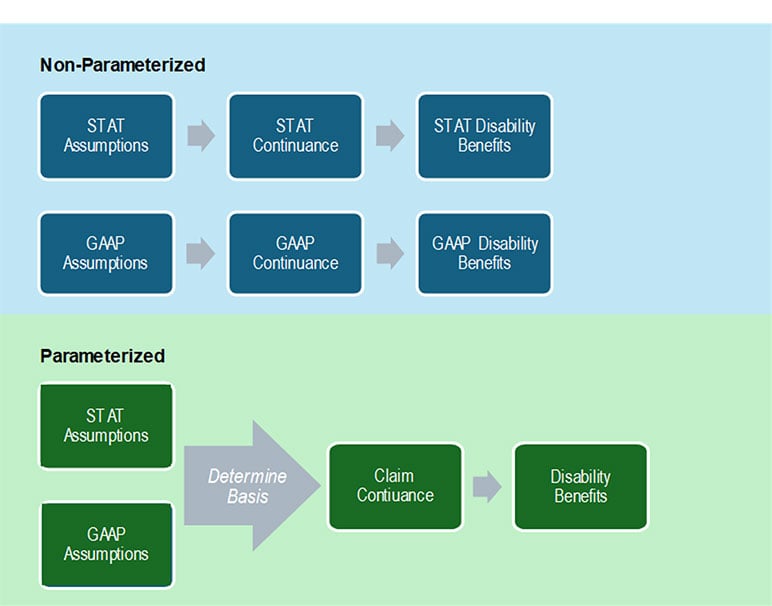
Step 3: In Figure 4, we take a step outside the claim termination rates calculation to highlight parameterized calculations. The model needs to project disability benefits under both Statutory (“STAT”) and GAAP bases. The formula for disability benefits is generally the product of the monthly disability benefit and the projected disabled lives. This calculation does not need to be programmed multiple times in separate STAT and GAAP variables (top portion of Figure 4) and instead, can be parameterized (bottom portion). The projected disability benefits can then flow into the reserve calculation under these two bases.

Figure 4
Projected Disability Benefits—Parameterized Calculations

Conclusion

Optimizing models is particularly relevant for open system models since the burden of process improvement falls on the open system model users. By optimizing models, we believe the following benefits can be achieved:

• Faster decision-making: Reduced runtimes empower management to make decisions more quickly. In addition, more sensitivities/tests can be run, allowing for more informed risk analysis.
• Improved close processes: During quarter-end and year-end close processes, valuation actuaries often run several models. Improved performance eases quarter-end and year-end processes, especially during intensive cash-flow testing cycles.
• Cost efficiency: Optimizing models by updating the underlying software should be less expensive than purchasing additional computing power (hardware).

Importantly, these benefits extend beyond insurers and their management—they directly improve the experience of all model users.

• This article is provided for informational and educational purposes only. Neither the Society of Actuaries nor the respective authors’ employers make any endorsement, representation or guarantee with regard to any content, and disclaim any liability in connection with the use or misuse of any information provided herein. This article should not be construed as professional or financial advice. Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries or the respective authors’ employers.

[i] There may be situations where modelers simplify calculations to improve runtime. However, these simplifications should be clearly justified and documented.

[ii] A cell may also transition from the disabled state back to the active state, which is known as recoveries. We have ignored recoveries in our illustrative case study.

[iii] Exhibit 1 loop size = (65-35) x 600 = 36,000 iterations. Exhibit 2 loop size = 12 x (30 + 29 + .... + 1) = 5,580 iterations.

1 - 5,580 / 36,000 = 85%. This derivation ignores any potential contractual benefit period guarantees.