By Paul Ramirez
In this excerpt from Mental Math, the authors describe a method to check that a list of numbers is summed correctly. This method is shown below:
MOD SUMS
If I’m not sure about my answer, I sometimes check my solution by a method I call mod sums (because it is based on the elegant mathematics of modular arithmetic). This method also goes by the names of digital roots and casting out nines. I admit this method is not as practical, but it’s easy to use.
With the mod sums method, you sum the digits of each number until you are left with a single digit. For example, to compute the mod sum of 4328, add 4 + 3 + 2 + 8 = 17. Then add the digits of 17 to get 1 + 7 = 8. Hence the mod sum of 4328 is 8. For the previous problem the mod sums of each number are computed as follows:
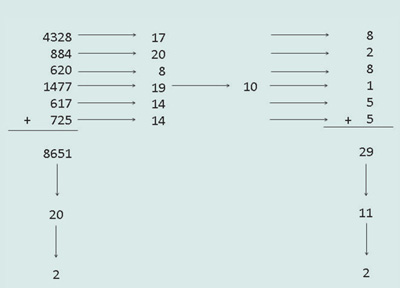
As illustrated above, the next step is to add all the mod sums together (8 + 2 + 8 + 1 + 5 + 5). This yields 29, which sums to 11, which in turn sums to 2. Note that the mod sum of 8651, your original total of the original digits, is also 2. This is not a coincidence! If you have computed the answer and the mod sums correctly, your final mod sums must be the same. If they are different, you have definitely made a mistake somewhere: there is about a 1 in 9 chance that the mod sums will match accidentally. If there is a mistake, then this method will detect it 8 times out of 9.
The mod sum method is more commonly known to mathematicians and accountants as casting out nines because the mod sum of a number happens to be equal to the remainder obtained when the number is divided by 9. In the case of the answer above—8651— the mod sum was 2. If you divide 8651 by 9, the answer is 961 with a remainder of 2. In other words, if you cast out 9 from 8651 a total of 961 times, you’ll have a remainder of 2. There’s one small exception to this. Recall that the sum of the digits of any multiple of 9 is also a multiple of 9. Thus, if a number is a multiple of 9, it will have a mod sum of 9, even though it has a remainder of 0.
From Secrets of Mental Math: The Mathemagician’s Guide to Lightning Calculation and Amazing Math Tricks by Arthur Benjamin and Michael Shermer, copyright © 2006 by Arthur Benjamin and Michael Shermer. Used by permission of Three Rivers Press, a division of Random House, Inc. Any third party use of this material, outside of this publication, is prohibited. Interested parties must apply directly to Random House, Inc. for permission.
To expand upon why this technique works, the authors are using modular arithmetic as noted above. If the tentative sum is not congruent to the list of numbers using modulo 9 (or any number, but 9 will be shown to be convenient), then the sum cannot be correct. The reason modulo 9 is nice is that a number can be reduced using modulo 9 by simply summing the individual digits as shown above. In a number, each digit represents that digit multiplied by a power of 10, depending on the position of the digit. In the excerpt, the 8 in 8,651 really means 8 * (1000) which can then be factored into 8 * (999 + 1). When this product is expanded, the 8*999 term is obviously divisible by 9, which results in a remainder of 8.
Paul Ramirez, FSA, MAAA, is a senior actuarial associate at Allstate Benefits. He can be reached at paul.ramirez@allstate.com.