The Syllabus as an Instructional Aid for Complex Problem-Solving
By Russell Jay Hendel
Expanding Horizons, August 2023

The course syllabus serves varied functions,[1] including being (1) a contract between the university, the instructor and the student; (2) a means of achieving uniformity and accountability across multiple sections of the same course taught by different instructors; (3) a means of evaluating the readiness of transfer students from other universities to take courses having certain prerequisites; (4) a means of evaluation of an instructor’s and institution’s compliance with required coverage of certain topics enabling various recognitions, statuses, promotions and certifications; (5) a permanent record that future faculty can use when teaching the course; and (6) a schedule of topics and exams to help instructors and students plan.
This article studies the syllabus as a dynamic, interactive teaching tool that informs and is informed by both solutions of complex course problems and student difficulties with these problems.
Two examples are presented:
- By considering the prerequisite sequence of modules and units needed to solve complex problems, the course problems can shape and help create the syllabus design.
- By skillfully using lessons learned in subtasking the component parts of a problem solution, the syllabus grows dynamically, enabling a significant increase in student learning, retention and satisfaction.
The techniques presented enable a deeper understanding of goal setting, the subtasking of component parts of a solution that is optimal for learning, retention and satisfaction.
The Fundamental Course Problem
Examination of the following reinvestment problem from the Society of Actuaries (SOA) Financial Mathematics (FM) course,[2] will guide us through the presentation of how a simple consideration of prerequisites can shape syllabus design.
Illustrative Problem: An investor who currently has $8,000 in a bank account borrows $2,000 for 10 years. The loan requires return of principal in 10 years and monthly payments (on the entire loan amount) of 6% compounded twice a year. The investor then pays $10,000 to purchase a 10-year bond with semi-annual coupons at an annual rate of 1.5%, and with a $9,000 redemption value. Calculate the yield to the investor of the total package.
To solve this problem, candidates (i.e., students) must already be familiar with the following prerequisite techniques:
- The candidate must be able to price (calculate the present value of) a stream of payments at periodic intervals for n years and to calculate the yield of such a stream of payments purchased at price P.
- The candidate, given a rate, must also be able to discount a single cash flow at time t, such as the $2,000 or $9,000 payments at time 10 to time zero.
- The candidate must be able to convert annual interest rates to non-annual payment rates.
- The candidate must be able to create an equation of value relating inflows and outflows.
- The preceding subproblems require a candidate—given an interest rate, a single cash flow C at time t, and another point of time t′ both to calculate the actuarially equivalent value of C at time t′ as well as to understand the meaning and application of actuarial equivalence.
Additionally, although theoretically the course can be taught successfully without these techniques, mastery of the following skills facilitates both arriving at solutions and improving their accuracy:
- The candidate is able to geometrically model a single or set of cash flows using labeled time-value lines.
- The candidate is able to use the BA-II Plus calculator to instantly derive any of the following five items given the other four: interest rate, present value, periodic payment, future value and number of periods. (While paradoxically, the official SOA FM syllabus does not require this calculator skill, or even require the BA-II Plus, it greatly facilitates the speed and accuracy of doing a problem.)
Prerequisite Sequence Paths
Applying a single, modest syllabus-construction principle—prerequisites should be taught and mastered prior to the modules that use them—to the illustrative problem already yields the syllabus unit sequence presented in Figure 1.
Figure 1
The Syllabus Sequence Implied by the Illustrative Problem
The asterisked items in this sequence refer to syllabus units that must be revisited and updated periodically. For example, an instructor might teach the Time Value–Calculator line first for single investments, then later revisit it when teaching periodic payments, then revisit it again when teaching annuities (which is the first time the periodic payment key is used), and then revisit it yet again when teaching sinking funds and bonds (which combine the use of periodic payments and single payments).
In the sequel, we will refer to such syllabus-unit sequences as prerequisite-sequence paths. We will refer to the problems that generate these paths, such as the reinvestment problem, as fundamental course problems.
An analogy may help to clarify these definitions. The curriculum path of Figure 1 is reminiscent of the critical path in the PERT diagrams of operations research.[3] More generally, one can model the units of the course using graph theory, where the points of the underlying course graph are units of the course, and the directed edges represent prerequisite dependency. This technique can be summarized by asking the instructor to identify paths of maximal length (the diameters) of the underlying graph. The point of the analogy is that, just as in operations research, the critical path is important in allocating times to subtasks of a project; in syllabus construction, the fundamental prerequisite path is important in defining the units and modules of the syllabus.
The Syllabus as an Instructional Tool
The prerequisite-sequence path of Figure 1 has already shown how the syllabus can be used as a pedagogical aid and instructional tool, but the following are also equally important benefits.
- Motivation: Prerequisite-sequence paths naturally suggest the motivational technique of anticipating goals. That is, when teaching earlier, less glamorous parts of the course, the instructor might whet student appetites by presenting the fundamental course problem(s) and indicating that the current unit will help in solving it. Since fundamental course problems are typically live, real-world applications, they naturally motivate.
- Foreshadowing[4]: Knowledge of which fundamental course problems will be used in a course allows an instructor to skillfully foreshadow the solution components of these problems in earlier units of the course. For example, while teaching annuities, one can ask, “Compute the present value of a sequence of periodic semi-annual cash flows each equal to application of a 6% rate convertible monthly to $2,000,” foreshadowing the fundamental course reinvestment problem. The resulting creation of familiarity with the components of problems to be presented later in the course facilitates teaching these problems. Knowledge of how prerequisites will be used assists in selectiing problem difficulty in earlier units of the course; the earlier course unit problems should not be given just for practice but should mirror the difficulty of similar problems used later.
The Syllabus as a Goal-Setting Tool
The second example of this article, that of the syllabus as an instructional tool, is deeper. To fully appreciate it, we first review goal setting.
Goal setting is the technical term by which the literature refers to breaking up a complex problem into component parts. Good or optimal goal setting refers to goal setting that maximizes learning, retention and satisfaction. Since both the business and academic worlds heavily involve complex projects, knowledge of how to optimally set goals—that is, to maximize learning, retention and satisfaction in the educational world and maximize productivity and efficiency in the business world—is the subject of extensive research.
Many instructors are already familiar with the SMART acronym, which requires tasks in optimal goal setting to be specific, measurable, attainable, realistic and achievable in a short time. A closer examination of the literature suggests five more attributes of optimal goal setting: clarity, challenge, commitment, feedback and task complexity. These ten attributes naturally group into three main categories: specific, challenging and achievable in a short time.[5]
The Goal-Setting Paradox
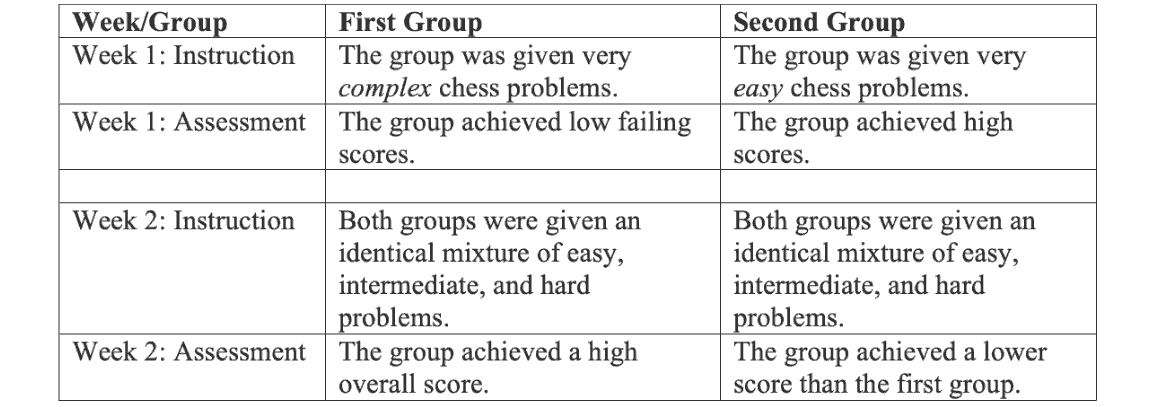
The following beautiful and remarkable experiment from the 1970s illustrates what has come to be known as the goal-setting paradox.[6]
Two groups of college students not familiar with the game of chess were recruited for the experiment. The groups, after being taught the moves and rules of the game, were assessed for their ability to solve chess problems. Table 1 summarizes the assessments and results.
Table 1
Summary of Instruction and Assessments of Problem-solving Ability of Two Groups
We can summarize this experiment, illustrative of the goal-setting paradox, as follows. By giving the first group problems so challenging that they could not solve or learn, they achieved a higher level of understanding and learning as evidenced by the assessment at the end of week 2.
This experiment (correctly) suggests and confirms the criteria for optimal or good goal setting: syllabus units, in addition to being specific and clear, should simultaneously be challenging and achievable in a short time. Clarity and specificity by themselves are not sufficient to assess the correctness of a syllabus unit. To consider the extremes of what could go wrong if relying solely on clarity, note that (1) if the subtasks are too easy, students are unmotivated and lose interest in learning; and (2) if the subtasks, while clear, are too few, students may be overly challenged, leading to confusion and lack of direction on where to begin. In both cases learning, retention and satisfaction are inferior.
The requirement of a simultaneity of both challenge and achievability leads to the motto that teaching is an art, not a science. It is not enough to be logically and cognitively correct; rather, the syllabus units must simultaneously challenge and allow mastery. This balance of challenge and achievability, the goal-setting paradox, requires a feel for the students, for what is too easy, too hard, and just right.
To meet these goals, this author’s personal experience and general practice is that each unit and each class and practice problem intrinsically involve at least two subproblems; require the use of multiple mental modalities for solution (e.g., verbal, geometric, algebraic and calculator [the rule of four]); and must be specific, for example, by avoiding open-ended problems of a research nature.[7]
An Illustrative Example
The following example from teaching the SOA Financial Mathematics course illustrates how critical goal setting is for performance; how teaching is an art; and how a partnership between instructor and students is necessary to optimize learning, retention and satisfaction.
While the beginning modules of the FM course require calculations of present value under conditions of level interest rates, later modules address the more realistic use of spot rates and forward rates. Having taught these, the instructor then revisits pricing problems done earlier in the course such as the following.
A company is planning to engage a year from now in a transaction that will pay $1 million and $2 million at the end of the second and fifth year of the transaction. Price this transaction (present value) at the time of transaction using spot rates currently available in the market.
Letting v(t) indicate the discounted value of $1 t years from today under the current term structure, the equation of value for the problem just cited is
P v(1) = 1 v(3) + 2 v(6),
with P indicating the present value at t = 1 under the current term structure.
Even though equation 1 avoids calculation of forward rates by only requiring consideration of spot rates and the consequent discount factors, nevertheless, similar problems presented on the actuarial software of companies assisting students to prepare for exams assess this type of illustrative problem as difficult. Typical examination papers in the author’s courses show a variety of student errors: confusion of v(i) with vi or the distortion of forward rate formulas into nonsensical formulas. It is sometimes difficult to give even partial credit.
The author solved the instruction of this problem using the principles of goal setting. Too many new concepts—variable rates, spot rates, implied forward rates, non-power discount functions—are being thrown at students, who do not have sufficient time to absorb and master them.
Good goal setting suggests a solution: if something is too challenging, simply break it up. Consequently, the author broke the solution into two parts: (1) Students are given a term structure and are asked to create a table with three more rows with implied discount factors, present values of $1 zero coupon bonds maturing in t years, and the one-year forward rates. (2) The students are then asked to use the table they developed in part (1) to create equation 1. To “trick” the students into complying with doing the problem in two steps versus all at once, they are told that a correct answer to the second part based on an incorrect answer obtained in the first part would not be penalized. This simple goal-setting approach sufficed to totally reverse performance; students now routinely get these problems correct.
This vignette illustrates the type of give-and-take between the instructor and students that must take place to achieve proper goal setting. One could not theoretically predict that a two-step solution would optimize teaching and learning. It required class experience, as well as knowledge of the goal-setting and syllabus construction tools, to recognize the instructional issue and the approach to a solution.
Conclusion
Other instructors are encouraged to incorporate the ideas of this article—allowing problems, the syllabus and student difficulty to inform each other—in their instruction.
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the editors, or the respective authors’ employers.
Russell Jay Hendel, Ph.D., ASA, is the chair of the Education and Research Section council. He is adjunct faculty III at Towson University, where he assists with the Actuarial Science and Research Methods program. Russell can be reached at RHendel@Towson.edu.