VM-20 Company Experience Mortality Rates: APF 2020-08
By Tim Cardinal
The Financial Reporter, April 2021

My article “VM-20 Game Changer: Mortality Aggregation,”[1] considered the 2020 edition[2] of the Valuation Manual’s incorporation of Amendment Proposal Form (APF) 2018-17. VM-20 permits data aggregation to enhance credibility with an “if similar” requirement—aggregated segments have similar underwriting processes and similar mortality. VM-20 then requires that company experience mortality rates are “informed” by the aggregate experience using one of two prescribed methods: Section 9.C.2.d.vi.a and b are called the “top-down” and “bottom-up” methods respectively. However, both methods have shortcomings when a company’s mortality assumption is highly granular resulting in a large number of segments. As a remedy, I submitted APF 2020-08 proposing a third method called the “two-step.” The Life Actuarial (A) Task Force unanimously passed APF 2020-08 in November 2020 and thus it will likely be adopted in the 2022 edition of the “Valuation Manual.”
Bottom-Up and Top Down Methods
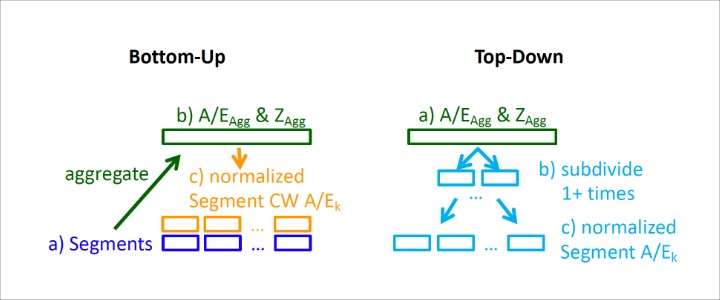
As illustrated in Figure 1, the bottom-up method starts with each segment (the bottom), aggregates all segments to determine the aggregate’s A/EAgg and credibility factor ZAgg, and then credibility weights (CW) each segment’s A/Ek with A/EAgg using k’s credibility factor Zk as weight:
(1) Segment k’s CW A/Ek = (1 - Zk) × A/EAgg + Zk × Segment A/Ek.
The top-down approach starts at the aggregate (the top), and then subdivides one or more times into more granular subgroups until the segments are reached with each subdivision using predefined expected relativities between subgroups based on reliable and applicable external sources. Both methods modify (informs) our view of the segment A/Ek compared to the initial A/Ek. That is, both methods produce rates that are different from a stand-alone study on policies belonging to each segment. The final requirement for segment A/Ek is conservation of deaths which is represented using normalization.
Figure 1
Bottom-Up and Top-Down Processes
Shortcomings
Some companies have highly granular mortality assumptions for pricing, business forecasts, and risk management. It is desirable that VM-20 company experience mortality rates correspond to assumptions for pricing and other purposes in regards to granularity and A/Es (before consideration of margins). Consider highly granular contexts, e.g., a block with 360 mortality segments determined by two sexes × six risk classes × five face bands × three product types × two underwriting types (such as full and accelerated). Consider further that the company has high credibility at lower levels of granularity, for example, across both sexes, full underwriting, most risk classes, and product types. In other words, the company uses its own data in setting assumptions and selectively supplements with external data and studies.
Both methods could produce company experience mortality rates that negate the very reasons a company uses high granularity. Most of the 360 segments likely have Zk near 0. Using a bottom-up method, Equation (1) and Zk ~ 0 imply that CW A/Ek ~ A/EAgg. Thus, all segments use A/EAgg which is equivalent to no granularity. A top-down method starts at the aggregate and then imposes external views that may be less relevant instead of starting where the internal views need to be supplemented.
APF 2020-08 Two-Step Method
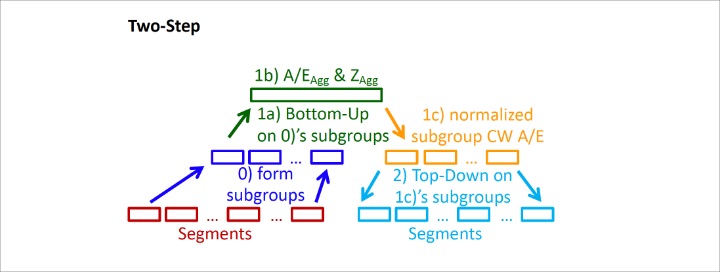
APF 2020-08 adds a third permissible method that generalizes the bottom-up and top-down by applying each method in sequential steps, hence I coined it the“two-step” method. Refer to Figure 2 below.
Figure 2
Two-Step Process
Step 0: As a preliminary step, form subgroups that are groups of mortality segments and are subsets of the aggregate class of mortality segments being aggregated, e.g., in the previous example form 12 subgroups as determined by two sexes × six risk classes. Each subgroup consists of 30 segments by combining face bands, product types and underwriting types under each sex and risk combination.
Step 1: Apply the bottom-up method to adjust the experience of each subgroup from Step 0 to reflect the aggregate and conserve deaths.
Step 2: Apply the top-down method to further subdivide the subgroups’ adjusted experience from Step 1 into the various mortality segments while conserving each subgroup’s deaths determined in Step 1’s conservation of deaths.
It is critical that Step 2’s starting point is Step 1’s modified view of the subgroups experience (i.e., subgroups normalized A/Ej) and not Step 0’s initial view. The two-step method is more robust drawing upon the bottom-up and top-down strengths while mitigating their weakness. Top-down is a special case of the two-step where there is one subgroup equal to the aggregate. Bottom-up is a special case where each subgroup is one segment.
Although each subgroup in the preceding example has the same number of segments, the two-step method does not require equal-sized subgroups. By judicious choices of subgroups, a company can balance internal views with credible data at various levels of granularity and supplement with external data and views where needed or desired. Thus, the two-step method provides flexibility. A company can define subgroups differently for two aggregation groups, e.g., simplified issue and full underwriting. Companies with differing degrees of experience and granularity needs or companies using experience data from other sources (i.e., external to the company) can choose their subgroups appropriately.
Miscalculations or execution risk is present in all three methods. A common mistake is that the aggregate does not inform the segment’s rates. This often entails the appearance of informing via many sub-calculations or use of many factors but in essence merely goes through a circuitous route to arrive at the individual mortality segment experience. Mistakes were sufficiently prevalent that the NAIC published a spreadsheet with examples illustrating correct and incorrect ways. APF 2020-08 expanded the NAIC examples to include Examples 8 and 9 as a correct and an incorrect way respectively to apply the two-step method. Refer to the principle-based reserving (PBR) data mortality aggregation tool on NAIC website[3].
Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the editors, or the respective authors’ employers.
Tim Cardinal, FSA, CERA, MAAA, MBA, is principal at Cardinalis 1 Consulting LLC in Ohio. He can be reached at tim.cardinal@cardinalis1.com.